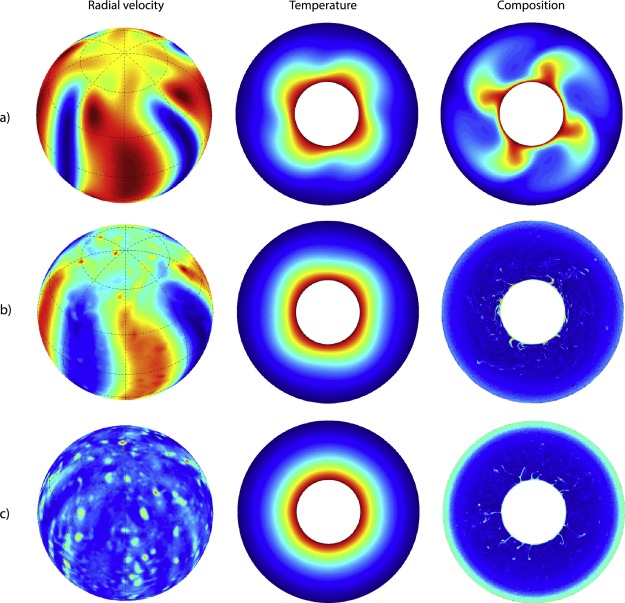
Mathieu Bouffard’s paper published in J. Comput. Phys.

At the beginnig of the summer, Mathieu’s paper was definitely accepted by the Journal of computational Physics (abstract and reference) and the final version appeared online on June 27th. You can access the online version. Mathieu has developed a tool to properly model solute transport in a rotating spherical shell, using PARODY-JA as the base for convection and dynamo. The code has been benchmarked and we obtained new results for the infinite Lewis number case, i.e. neglecting solute diffusion. This leads to the formation of very thin filamentary plumes.

For more details and applications, read the paper and come to Mathieu’s PhD defence on September 20th! it will be at 2pm in the big room of the library on the La Doua campus.

Snapshots of the radial flow field on a spherical surface at mid-depth in the shell (left column), equatorial sections of temperature (middle) and composition (right column) at time t = 2.1. (a): Le = 10, δ = 0.8; (b): Le = ∞, δ = 0.8; (c): Le = ∞, δ = 0.2.